[单选题]
甲乙两人同时沿直线跑道两端匀速相向而行,两人第一次迎面相遇时距跑道中点50米,两人到达跑道尽头时立即掉头重新出发,重新出发后两人第二次相遇,第二次两人相遇也为迎面相遇,且距跑道中点150米。则此时两人中速度较快一人比速度较慢一人多行走多少米?
A . 150
B . 400
C . 200
D . 300
参考答案: D
小麦参考解析:
第一步:判断题型------本题为行程问题
第二步:分析作答
如图所示: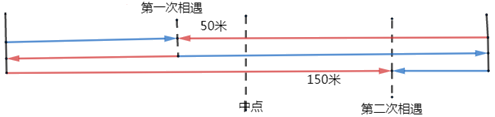
设跑道全称为2S,则半程为S;
如上图所示,第一次相遇时,速度较快的人走的路程为S+50米,速度较慢的人走的距离为S-50米;
根据多次相遇公式,第二次相遇时,速度较快的人走的路程为(S+50)×3=S+150米,速度较慢的人走的距离为(S-50)×3=3S-150米;
则速度快的人比速度慢的人多走:(3S+150)-(3S-150)=300(米);
故本题选D。
【2021-新疆兵团行政执法-054】



