第一步：判断题型------本题为概率问题

第二步：分析作答
设绳子长为a，三段分别为x、y、a-x-y，且0<x<a，0<y<a，0<a-x-y<a（即0<x+y<a），则根据这三个约数条件可画出取值区间如下图△OAB所示，（其中AB线段表示0<x+y<a）。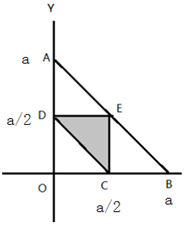

要构成一个三角形，则需满足两边之和大于第三边，因此可列下式：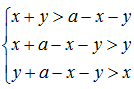
，
即；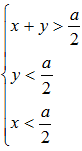
取值区间即为图中阴影部分△CDE。
因此所求概率为灰色△CDE面积占△OAB面积的比值，为。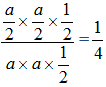

故本题选A。
【2019-江苏A-064】