第一步：判断题型------本题为概率问题

第二步：分析解题：
方法一：
设线段长度l=1，所截三线段长度分别为x、y、1-（x+y）。
根据三角形两边之和大于第三边列方程：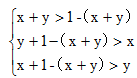
；
化简得：；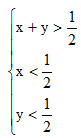
又x>0，y>0，1-（x+y）>0；用图形表示如下：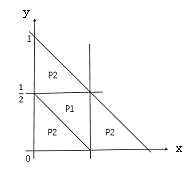

则p1为所截的三线段能构成三角形的概率，即等于中间三角形的面积；
p2等于大三角形面积减去中间小三角形的面积。
故p1=1/4，p2=1-1/4=3/4，p1<p2。

方法二：
设l=1，由三角形三边关系“两边之和大于第三边”可得：
当其中一段长度≥0.5时，不能构成三角形。
一条线段截成3段需要截2次，先任取一个点截第一次，那么第二次截取的点与第一次位于中点同侧或不同侧的概率均为，分类讨论如下:
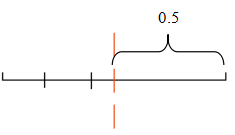
当两个截点在线段中点同侧时（包括中点），如下图所示，两个截点中的任意一个与另一侧的线段端点之间的距离即所截的三线段某一段必然≥0.5，则不能构成三角形，即；

当两个截点在线段中点在不同侧时，有可能两个截点之间的长度≥0.5，如下图所示，此时截成的三条线段将无法构成三角形，即。

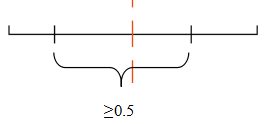
综合以上两种情况，，而P1+P2=1，则P1<P2。

故本题选C。
【2018-江西-067】