(单选试题)
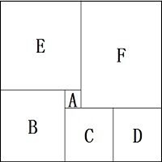
一个箱子的底部由5块正方形纸板ABCDE和1块长方形纸板F拼接而成(如图所示),已知A、B两块纸板的面积比是1:16,假设A纸板的边长为2厘米,则该箱子底部的面积为( )平方厘米。
A、
200
B、
320
C、
360
D、
420
正确答案:C,正确率:65%,作答次数:701
能看懂解析
看不懂解析
收藏
纠错
答案解析
第一步:判断题型------本题为几何问题
第二步:分析作答:
A、B两块正方形纸板的面积比是1:16,则其边长比是1:4。
A纸板的边长为2厘米,所以B纸板的边长为8厘米;
除F外其他的均为正方形,所以E纸板的边长为8+2=10cm;
C与D的边长为8-2=6cm,F纸板的长为10+2=12cm,宽为2×6-2=10cm;
所以箱子底面的长为8+6+6=20cm,宽为12+6=18cm;
直接计算底面面积为20×18=360平方厘米。
或用整除法判断,底面面积能被18整除,只有C项满足。
故本题选C。
【2018-广东-024】
视频解析

评分:
还没有人评价哦,试试发表评价吧
评价列表
发表评价

来源
 陕公网安备 61010302000399号
陕公网安备 61010302000399号