(单选试题)
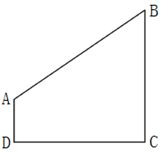
某市规划建设的4个小区,分别位于直角梯形ABCD的4个顶点处(如图),AD=4千米,CD=BC=12千米。欲在CD上选一点S建幼儿园,使其与4个小区的直线距离之和为最小,则S与C的距离是:
A、
3千米
B、
4千米
C、
6千米
D、
9千米
正确答案:D,正确率:37%,作答次数:643
能看懂解析
看不懂解析
收藏
纠错
答案解析
第一步:判断题型------本题为几何问题
第二步:分析解题:
由于在CD上选一点建幼儿园,故S到C、D两点间距离不变,只需满足AS+BS最小即可。
过CD作A点的镜像点A',连接A'B交CD于S,如下图所示: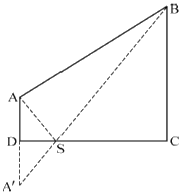
此时AS+BS=A'S+BS最小。
此时![]() ,即
,即![]() ,已知AD=4,CD=BC=12,解得CS=9。
,已知AD=4,CD=BC=12,解得CS=9。
故本题选D。
【2017-江苏A-069】
视频解析

评分:
还没有人评价哦,试试发表评价吧
评价列表
发表评价

来源
 陕公网安备 61010302000399号
陕公网安备 61010302000399号